THE VORTEX
(Formation and Properties of a Vortex)
Copyright (C) 1999, 2000, 2001, 2002
by Lew Paxton Price and Herbert Martin Gibson
Seneca
Back - Main Menu
There must be certain conditions for a vortex to form. Once formed, a vortex has certain properties. These conditions and properties follow.
CONDITIONS NECESSARY FOR VORTEX FORMATION
1. A large expanse of fluid must exist which will form the "body" of the vortex.
2. The fluid must have the quality of inertia. Nature of Inertia
3. The fluid must be under pressure.
4. A relatively small volume of lesser pressure must exist within the expanse of fluid to act as the vortex center.
5. This center must be capable of remaining a relative vacuum for the duration of the vortex.
6. This center must be capable of causing the fluid flowing into it to turn at ninety degrees to the inward directions of flow.
PROPERTIES OF A VORTEX
1. The mass of the fluid moving inward at any given distance from the vortex center equals the mass moving inward at any other given distance from the vortex center.
2. The mass of fluid moving into the vortex center at any given distance from that center is accelerating toward that center.
3. The inward instantaneous velocity of fluid flow at any given distance from the vortex center is equal to the tangential instantaneous velocity of fluid flow at that distance. "Instantaneous velocity" is used here because true velocity does not exist where there is only acceleration.
4. The resultant instantaneous velocity of fluid flow at any given point from the vortex center is at 45 degrees to the radial crossing that point.
5. The inward acceleration of fluid flow at any given distance from the vortex center is equal to the tangential acceleration of fluid flow at that distance.
6. The resultant acceleration of fluid flow at any given point from the vortex center is at 45 degrees to the radial crossing that point.
The reasons and proofs for the foregoing conditions and properties are found in the series of books called Behind Light's Illusion. They are too lengthy to place here.
THE DYNAMIC ETHER VORTEX
Although largely ignored by theoretical physicists, there is a question that has not been satisfactorily answered regarding the mass-energy equation usually attributed to Einstein. The question is: Why is the mass-energy equation E = mc2 while the kinetic energy equation is Ek = mc2/2 ? If energy from the annihilation of mass is truly energy, then it should be kinetic in nature. Yet, it is double the amount of the kinetic energy that one would expect it to be. Why isn't the mass energy equation E = mc2/2 instead of E = mc2 ? The following provides an answer to this question and links the heretofore mysterious world of subatomic matter and energy to our macroscopic world of mass and kinetic energy.
In a universe of dynamic ether, a vortex would be formed of this ether.
Light would be a transverse wave of accelerating ether caused by a vortex (electron) moving first one way and then the opposite way in a cyclic manner. A so-called photon would be a "package" of waves moving outward like ripples on a pond.
Planck's constant would the quantum for the passage of one wave - the accelerations of ether in two half-waves.
What we now call "mass" would be the amount of ether "Mass" moving into the vortex within a given length of time (such as one second).
The resultant inward acceleration of ether at any point would be at 45 degrees from a radial passing through that point.
A light half-wave would move straight outward at a velocity of "c" and would be a tangential acceleration of ether equal to c/t where t equals time.
The actual reaction speed of the ether is the resultant of the maximum inward acceleration vector and the maximum tangential acceleration vector. At any particular point in a vortex, the maximum inward acceleration vector is equal to the maximum tangential acceleration vector. When an electron is at rest relative to the surrounding ether, these maximums occur at the point where the inflowing medium turns at 90 degrees which is near the vortex center. This is where the highest vortex energy exists.
The following illustration shows the electron as it would appear from the top of the vortex. The large circle is the "hole" into which the medium is flowing. The curves lines are the paths taken by the medium which is also flowing into the plane of the circle. The tangential and radial speeds at this point are that of light, "c", and the resultant inward flow has the speed of the product of the square root of two and "c".
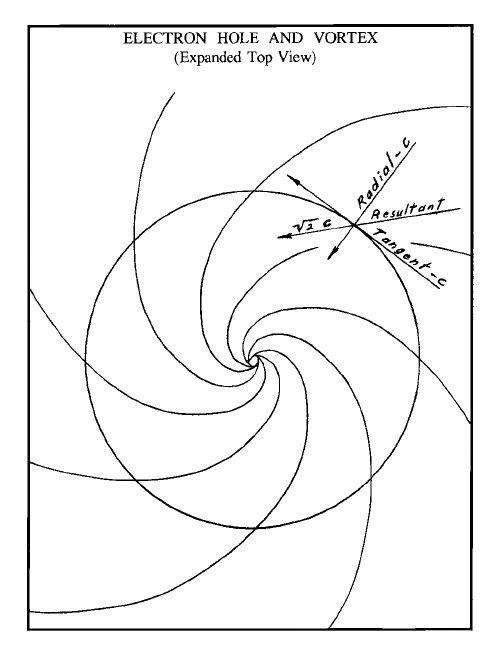
Both maximum accelerations are equal to c/t. The two maximums are at 90 degrees to one another. A right triangle is formed with the maximums as the sides and the resultant as the hypotenuse. The resultant is the maximum acceleration for the actual inward flow at this point and is the actual maximum reaction speed of the ether.
The maximum reaction speed of the ether is also the maximum instantaneous velocity that can be achieved by the ether flowing into a matter vortex. So the right triangle can also be used for instantaneous velocity which will allow us to calculate the maximum kinetic energy of the inward flow.
Using the Pythagorean theorem, for a 90/45/45 degree triangle with sides equal to c/t, the sum of the squares of the two sides is 2c2/t2. So the hypotenuse is equal to the square root of 2 multiplied by c/t. This may be written as 2 to the 1/2 power times c/t, or 21/2c/t.
The hypotenuse is the resultant. So the maximum ether acceleration would be equal to 21/2c/t. Numerically, this would also be the maximum ether instantaneous velocity (21/2c) found at the vortex center where the ether flow turns at 90 degrees.
When an electron and a positron meet, the inflow of ether into both ceases and they are destroyed. The sudden cessation of ether flow into these vortices causes the kinetic energy of the ether inflow to be released. This *destruction of the electron vortex when the electron is at rest releases ether kinetic energy, Ek. The release of this energy can be calculated as follows:
v = 21/2c = maximum instantaneous velocity of the inflowing ether
m = M/t = electron mass = total Mass moving into the electron vortex in one second
Ek = (1/2)mv2
Ek = (1/2)m(21/2c)2
Ek = (1/2)m(2c2)
Ek = mc2
[*This means for the destruction of the electron vortex only. For both electron and positron destruction, the energy release is doubled.]
E=mc2 is the mass/energy equivalency now attributed to Einstein. However, according to a website by Marcus Coleman visited in about 1999, www.wbabin.net/physics/marcus.htm, this equation was not Einstein's except by acceptance. In substance it was the work of Henri Poincare' (1900) and was correctly derived by Max Planck in 1906. Einstein gave credit to Planck once in 1906 and never did do so again. Furthermore, the equation is not uniquely dependent upon Einstein's theory of relativity and was first formulated simply by Pauli in 1920. It can also be derived from the pressure of radiation. Therefore, the equation is not the exclusive result of the precepts of general relativity and does not actually prove that Einstein's relativity is correct.
I can vouch for the fact that the equation can be derived from the pressure of radiation. As is shown above, it can also be derived as a consequence of matter being composed of ether vortices. This particular derivation is not a proof unto itself, but it is another fact implying that matter has such a composition.
More on Energies in the Electron Vortex
The kinetic energy of the vortex is what remains when the "hole" creating the vortex is closed. It is equal to mc2 as shown above. Kinetic energy must be equal to potential energy. The centrifugal force used to hold the hole open for the vortex to form is mc2/r. The energy used to open the hole is the same as the potential energy that would erupt were the hole to be closed. It is (mc2/r)r which is mc2 because energy equals force multiplied by the distance over which it acts. So we can see that in a nether vortex such as the electron, Ek = Ep = mc2 where Ep is potential energy.
Gravity at the vortex center would be shown by the equation g = c2/2r
where "g" is gravity and "r" is the radius at the electron center.
Kp = mgr = m(c2/2r)r = mc2/2. This is the
potential energy of mass or Mass at the electron center prior to a fall to the
exact center of the vortex from the vortex periphery. Note that it is half
of the total kinetic and potential energy of the vortex were the hole to close
suddenly. This is the potential energy due to gravity.
However, there is also the tangential component of mass or Mass that is moving at velocity "c". This also has a potential energy that is equal to that due to gravity. The two potential energies, the one due to gravity and the one due to the tangential component (angular momentum) total the same as the kinetic energy for the vortex (which is mc2).
mc2/2 + mc2/2 = mc2