MORE ABOUT THE ELECTRON
Advanced Electron Theory
Updated April 2, 2014.
Back - Main Menu - Confirmation of Light as Waves
The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings
There are many types of units in the world for many purposes and few of them agree. The first step in working with units is to convert to one system. This can be very time-consuming and is made even more difficult in a system which uses the same word for two different things. Therefore, when applicable, I show which thing that a particular unit is.
See Radio for more details on how systems of measurement differ between electrical theory and other disciplines.
In the final summary, the "knowns" herein will not be given to the last computed digit to the right of the decimal. They will be given to only four digits to the right of the decimal. This is not the most accurate way to show them, but every book seems to have a slightly different version of each number (or of the inputs for each number) after the first four are shown. This makes the first four to the right the only dependable ones.
Knowns
Speed of Light = c = 2.9979x10 8 meters/second
Electron Mass = me = 9.10956x10 -31 kilogram
where the *kilogram is a unit of mass
Planck's Constant = h = 6.6252x10 -34 joule second
= 6.757704x10 -35 meter
kilogram second
where the *kilogram is unit of force
The units for Planck's constant are flawed. See Planck's Constant.
Planck Unit of Action = h = h/(2pi)
= 1.0544x10 -34 Joule second = 1.075523x10 -35 meter
kilogram second
where the *kilogram is a unit of force
Planck Area = Ap = 2.66412388x10 -71 meter 2
Planck Length = Lp = 5.16151517x10 -36 meter
Gravitational Constant = G = 6.6742x10 -11 meter3/kilogram second2
where the *kilogram is unit of mass
*The metric system has the same name for force as for mass, unlike the English system which uses pounds for force and slugs for mass. The metric system was devised to create a standard that was "natural". Actually, the metric system is erroneous as to the "natural" part and fails to properly address the difference between force and mass. Perhaps it could be improved by calling the force unit a "Kram" and keeping the mass unit as the "gram". But truthfully, all of our current systems should be converted to new system that is more acceptable to all of the scientific/engineering disciplines.
(Some people spell the name Schwartzschild.)
Introduction - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings Schwarzschild radius = rs = 2Gm/c2
The Schwarzschild radius is the radius for any particular mass from which light cannot escape. It was originally derived for black holes, and was derived in nether theory with much less effort. With one modification, it seems to be able to work for electron mass as well as the masses of larger entities.
At the vortex center (the "hole"), nether enters at the speed of light, so it is the electron rs that is the approximate radius of the electron "hole" into the 4th dimension. It is true that the electron rs is well above the necessary energy level that particle physicists can reach with their accelerators, but what could they find if they were able to reach this level? The electron rs is computed via the equation above and is about 1.3529559x10 -57 meter.
New "Known"
Electron Radius at "c" according to the Schwarzschild Radius = rs = 1.3530x10 -57 meter
Introduction - The Schwarzschild Radius
The Light Equation - Finding ts - Finding n - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings The term "mass" that is used in physics today is actually the amount of nether "Mass" entering the hole into the 4th dimension in a unit of time. In most calculations for the same type of vortex, the particular unit of time is not very important because mass is a measure of flow. So mass can be equal to any value of M for the correct time in which it enters the hole. For example, if Mg enters in time tg, m = Mg/tg. If the time Mg is doubled, then so is tg, and the value of "m" does not change. During each time some of the incoming nether moves once around the vortex circumference at rs, more Mass enters the vortex. This means that the "mass" of an electron is a flow that does not change due to it happening within any particular period of time. If the mass (flow rate) is limited by time, then the "mass" or "Mass" for that time can be used as a unit. For instance, for one second of time,
m = (M/t) multiplied by one second = Mass or mass for one second of flow.
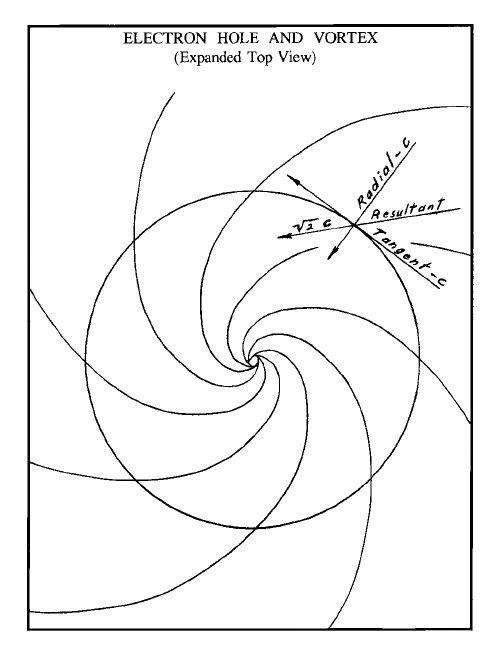
At rs, both the radial inward and the tangential velocity vectors of nether velocity equal the speed of light, "c". This means that the resultant of the two is equal to 21/2c.
The electron is a hole into the fourth dimension. It may be visualized by its construction. First think of a circular hole - just a circle hanging in the nether. If we look at the circle from its side, so that we see an infinitely small line, on one side of the line nether motion is essentially normal. On the other side, nether is flowing into the circle in the form of a vortex. The side with the vortex is the "mouth" of the electron.
The hole moves nether through it into the 4th dimension, so the mouth of the electron may point in any direction within our three-dimensional space and does so. When entering a magnetic field, the hole orients itself for minimum energy expenditure and its mouth pulls it to the right, left, up, or down, according to the way the magnets are set up. Less energy is expended in moving the electron toward the inflow than is expended in pulling all of the inflow toward the electron mouth. So in most cases, the electron moves in the direction that its mouth is pointed.
The vortex is formed of fluid elements moving at 45 degrees to any line (radial) from the vortex center. The speed of these elements, when near the electron center, is 21/2c, which is the square root of two multiplied by the speed of light.
As mentioned before, near the electron center the nether element velocity vectors parallel to the radials have a magnitude of "c", the speed of light. The nether element velocity vectors perpendicular to the radials are also equal to the speed of light. Kinetic energy equals (1/2)mv2. So the kinetic energy of the incoming nether at rs is (1/2)me21/2c2 where me is the rest mass of the electron. When simplified, this becomes mec2. This is based upon what would happen were the hole to close - which stops the inflow and releases the energy.
The speed of light is the incoming nether velocity because it is a vector pointing at 45 degrees from the resultant. The resultant of 21/2c is caused by the reactive acceleration of the nether moving from a place of nether higher pressure to place of nether lower pressure. In the kinetic energy equation, me is a measure of Mass flow and 21/2c is the actual resultant velocity.
The electron "vibrates" to create a natural "photon" of light. It moves back and
forth along a path. The electron moves along the path with its "mouth" forward to
conserve energy. At the end of the path, after each time that it turns to go back,
it creates a wave of nether acceleration that we call a light half-wave. During
the turning, the vortex is taking in nether at the speed of light and,
at the same
time, moving the nether tangentially at the speed of light. Of course,
the resultant velocity is
2 1/2c.
Saying this in other words, as it vibrates to create a series of electromagnetic waves (EM), the electron accelerates in one direction with its "pole" or "mouth" turned forward. It next decelerates (accelerates in the opposite direction) to a stop and begins to accelerate in the opposite direction while rotating 180 degrees so that its mouth is pointed forward again. As it accelerates and decelerates in its directions of movement, it is still taking in nether at a constant rate at 90 degrees to its directions of movement. The number of coils of incoming nether, n, just after it begins to accelerate each time are what cause a half-wave of light to have its particular value for Mass.
Therefore, n = cts/[(2pi)rt] is the number of vortex revolutions (circumferences) which can move into the "hole" in time "ts".
Back to Planck's Constant
Back to Light and Electron Spin
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
Finding ts - Finding n - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings Energy
The light equation and the mass/energy equivalency equation, E = mc2,
are both kinetic energy equations. It is true that
E = mc2 is supposed
to show the "rest" mass/energy for the electron, but the only thing that is
resting in this equation is the movement of the vortex relative to the nether
around it. The vortex itself is very active as it sucks in the nether.
There are two ways to show kinetic energy, shown here as "E". The way that we
are taught in school is with the equation
E = (1/2)mv2. This equation
is very misleading. Nothing that is moving ever squared its velocity. A baseball
in flight has kinetic energy due to its velocity we are told. The fact is, that
velocity is relative and the energy in the ball can only be known when the ball
hits something. Due the fact that motion is relative, it is just as proper
scientifically
speaking to think of the brick wall the board hits as moving toward the
ball while the ball is "at rest".
The energy that is supposedly due to the ball's velocity squared is removed when the ball hits the wall. The removal of the energy is a change. Change in this universe is accomplished only by acceleration, jerk, or a higher derivative of motion.
When the ball hits the wall it suddenly decelerates. Looking at it from another standpoint, the ball accelerates to a stop. The distance through which this acceleration occurs is very short, but nevertheless there is a distance through which it occurs.
The equation E = (1/2)mv2 is a mathematical shortcut that is handy to use, but extremely misleading when it becomes a supposed major fact. It came from the more "truthful" equation E = mad where "m" is mass, "a" is acceleration, and "d" is the distance through which the acceleration is applied. The mass of the baseball was accelerated to a stop through a very short distance.
If we carefully examine E = mad, we can see what happened to make it become E = (1/2)mv2.
E = m a d
Acceleration is distance divided by time divided by time.
E = m d/t/t d = m d/t2 d = m d/t d/t = m v v
"v" is velocity which is d/t. But the second velocity is not the same as the first. It is average velocity during the ball's acceleration to a stop. It is the first "v" plus the ball's velocity after it stopped, all divided by two: (v + 0)/2. This can be shortened to v/2 and the equation looks like this.
E = m v v/2
This, of course, is E = (1/2)mv2.
It is easier to use this shortcut when calculating because one need not worry about acceleration or distance. One need only worry about the mass and the velocity, both of which are much more easily measured.
The Mass/Energy Equivalency Equation
Back to Relativity
(Also called the Mass/Energy Equivalence Equation)
E = mc2 is another energy equation that is a mathematical shortcut. It is derived from the fact that nether is moving at its maximum velocity at the electron vortex center. This maximum velocity is caused by the reactive speed of the nether when it accelerates from a vicinity of higher nether pressure to a vicinity of lower nether pressure. Because we are dealing with a vortex, this maximum velocity is at 45 degrees to the inward velocity vector that creates the mass of the electron. It is also at 45 degrees from the vortex tangential velocity vector which is also "c". So the resultant magnitude of the vortex velocity is the product of the square root of two and "c".
vmaximum = 2 1/2c
The mass of the electron is actually a flow rate of nether Mass (with a big "M"). What we call "mass" is "Mass" per unit of time. A flow rate is a little different from a other quantities. Mass is flowing into the hole that creates the vortex. If we choose an amount of Mass that flows into the hole in one second as a standard, then our electron mass, "me", can be measured by Mone divided one second.
me = (1)M / (1) second
Dimensionally, this is m = M/t
Now if we double the amount of mass going into the electron, we have:
me = 2M / 2 seconds.
Tripling the amount of mass, we have:
me = 3M / 3 seconds.
The Mass changes and time changes, but the flow rate, me, does not change. The fact that the mass is flow rate is important in understanding the equations of the electron.
The maximum inward velocity vector at the electron center is the speed of light "c". This is what creates the actual flow rate rather than the resultant velocity of the nether at the electron center. But this velocity vector is merely part of the mass flow equation m = M/t, and does not enter into the energy/mass equivalency equation E = mc2 except as part of m.
It is best that we remember from the discussions on gravity, that the nether flow into the electron is actually an acceleration at all points within its little gravity funnel. The Mass has accelerated from zero velocity at a nearly infinite distance to a velocity of 21/2c at the electron center. So the average velocity is zero plus 21/2c all divided by 2.
Now we can better examine the energy equation for electron rest mass.
E = m a d
E = m (21/2c/t) (21/2ct/2)
E = m 21/2c 2/2
E = mc 2
The reason that electron mass can become energy according to the above equation is that the hole can close under certain circumstances and the kinetic energy of the incoming nether can be converted to electromagnetic energy (light), temporary smaller vortices, or other entities such as neutrinos. This energy is very different from the energy in the light equation because one is a stoppage of inflow and the other is a transverse acceleration of the inflow over a very short time.
Back to Electromagnetic Radiation
In the 1880's, Wilhelm Hallwachs and Heinrich R. Hertz discovered the photoelectric effect. This was analyzed further by later experimenters. Incident light can eject electrons from metals. The velocities of these electrons are independent of the intensity of the light but increase with its frequency. The number of electrons ejected per unit time is proportional to the intensity of the light.
Planck introduced his constant in 1905 to explain the distribution in frequency of radiant energy in a cavity of a body as a function of the temperature of that body. He found that he could derive the correct law of distribution with two assumptions: (1) each oscillator producing the radiant energy can possess only discrete amounts of energy or "nhf" where "n" is an integer, "h" is Planck's constant, and "f" is the frequency of that oscillator, and (2) the probability that an oscillator has the energy "nhf" is proportional to e - nf / kT where "k" is the Boltzman constant and "T" is the absolute temperature.
Bear in mind that Planck was experimenting with many oscillators (electrons) providing light in many frequencies over a period of time that was not exactly one second in duration. He was using temperature to measure the energy.
In 1905, Einstein proposed that the photoelectric effect was caused by light concentrated in bundles or quanta, of energy "hf", where "h" is Planck's constant and "f" is the frequency of the light. Each of the bundles can be absorbed only as a whole and by an individual electron. Thus the absorbing electron is given an additional kinetic energy equal to "hf". In passing through the surface barrier of the metal, the electron loses from this energy a portion which can be designated as "hfo". The kinetic energy with which the electron emerges is then given by:
Ek = (1/2)mv2 = h ( f - fo )
This gives the maximum energy of ejection, since electrons can also lose some energy inside the metal before reaching the surface. The equation indicates that unless "f" is greater than "fo" the electrons cannot escape, so there exists a low frequency limit for the ejection of any electrons. The equation gives no reference to the intensity of the light, but gives the energy of the ejected electrons in terms of frequency only. This expression, when later modified to take into account the various energies possessed by the electrons before they absorb the light, agreed with the results of the experiments in detail.
The author of some paragraphs in Encyclopedia Americana states: The equation itself, however, is completely paradoxical from the point of view that regards light as an electromagnetic wave and the electrons as charged material particles. [In nether theory, there is no such paradox.]
The next extremely important fundamental contribution which came from the field of X-ray research was made by Arthur Holly Compton in 1923. It had already been observed by Joseph Alexander Gray (1920) that short wavelength X-radiation, after scattering from carbon and other low atomic number atoms, was somewhat more absorbable than the primary radiation, but still of a "hardness" so clearly related to the primary radiation as to exclude its being a characteristic fluorescent radiation from the scatterer.
"Compton gave the following daring explanation of this effect. He supposed the bundles of radiation energy, "hf ", instead of being associated with spreading waves, to be propagated through space from the source in the form of projectiles. When one of these projectiles (or "photons"), each with momentum "hf/c", was scattered by a loosely bound electron in some low atomic number scattering material such as carbon, the electron would recoil under the impact, the more so the larger the angle of scattering and the higher the quantum energy (and hence the momentum) of the projectile. The kinetic energy thus given to the electron at the expense of the photon explained the "softening" of the scattered radiation in a completely and quantitatively correct way.
"Using characteristic line radiation from a molybdenum target tube, Compton showed that in the spectrum of the scattered radiation there appeared lines each of which was shifted toward longer wavelengths than its corresponding line in the primary radiation by an amount in complete accord with his theoretical explanation.
"The recoil electrons were also detected and shown by Compton and Simon to have the requisite
speeds and directions of recoil. Even more than this was ascertained, for Jesse W. M. Dumond
and Harry A. Kirkpatrick succeeded in showing that the shifted line above referred to was
notably broader than the unshifted line and this was satisfactorily explained by them
(with complete quantitative verification in all respects), to be due to the randomly directed
velocities possessed initially by the atomic electrons which were the agents that scattered
the photons. The presumptively dynamic character of the electronic clouds in atoms both for
gases and for solid metallic bodies was thus experimentally verified."
Planck's Constant
Force is the product of mass and acceleration.
F = ma
Energy is the product of force and the distance the mass is moved by the force.
E = mad
Power is energy divided by time.
P = mad/t
The "energy" equation for the photon is:
hf = m a d
If the number of waves in a photon is "n",
h(n/t) = mad
Then the equation for the lightwave (frequency of one) is
h(1/t) = mad : and for the half-wave is
h/2t = mad
"ts" is the time taken for an electron to reverse direction 180 degrees during light propagation. Two are necessary when speaking of a full wave of light. These short time intervals serve as limiters to me which is rate of nether flow, so that the correct flow for the period of electron turn-around is used in equations.
[The acceleration of "2c/ts" is not exactly a true acceleration because no particular Mass or mass is being accelerated faster than light. The incoming nether that is the "Mass" that creates what we call electron "mass" is being moved a small portion at a time to become a flow that began at "c" in one direction and ended at "c" in the opposite direction - all in time "ts".
The fraction of mass that is moved during "ts" is "me(ts/t)".
So in "mad"
"m" is [me(ts/t], "a" is 2c/ts, and "d" is cts/2 which is also (2pi)rsn/2.
For a frequency of one, the full wave energy is "h(1/t)", and for the half-wave the energy is "h/(2t)".
h/(2t) = [me(ts/t)](2c/ts)(cts/2).
When simplified, this is:
h/(2t) = [me(ts/t)]c 2
which can derived also from the other energy equation
E = (1/2)mv 2.
The half-wave passage relative to the observer is in two parts, one on each side of what might be called a centerline. One part is half of the half-wave energy and the other part is the other half of the half-wave energy. If the average velocity were used with the two halves together, the result would be zero because one side is the mirror image of the other and the velocities cancel one another. So one side must be computed and then multiplied by two for the total. The equation for one-half of the half-wave energy is:
h/(4t) = (1/2)[me(ts/t)]c2
which, when multiplied by two for the complete half-wave energy is
h/(2t) = [me(ts/t)]c2
If both sides of the above equation were divided by "c" as would be the case with Compton's equation for momentum:
h/(2ct) = [(me(ts/t)]c.
Which in dimensional analysis is momentum "mv".
Since (ts/t) is actually a dimensionless fraction, dimensionally h/2 and h would both be a form of energy when "1/t" is included within them - which is what I believed happened when they were discovered, the "t" being "one second" making it invisible. Of course, dividing by c provides a form of momentum.
So in a
strict sense, Planck's constant is
energy and Planck's constant divided by "c" is momentum.
When the "t" in frequency is introduced to a Planck's constant that is actually energy,
that energy is divided by time
and becomes a form of power. It would appear
that "h" should have had "1/t" included in its dimensions. Then, "hn" would have been the
energy for a photon, and "hn/t" would have been power (which is important when working with
red shift).
The Paradox
Kinetic energy is "(1/2)mv2" and momentum is "mv". Dividing me(ts/t)c2 by "c" does not result in momentum. To arrive at momentum, one must use "(1/2)c" as the divisor. So there are two possibilities.
1. Planck's constant must be half as large as it should be.
2. Momentum must be half as large as it should be.
Compton's "hf/c" is absolutely correct for the the momentum imparted from electron spin during an electron reversal such as is the case with a half-wave. For a full wave the change in energy is double. Possibly because of this doubling for energy, the momentum of Compton appears to be half what is normal.
Or perhaps Compton was measuring half of the half-wave for his momentum. Because the two halves of the half-wave oppose to one another, this is about the only way that momentum can be measured.
Compton's work in discovering momentum has been satisfactorily verified and appears to be correct. The Hallwachs and Hertz experiment in discovering the photoelectric effect is based upon proportions rather then absolutes. The velocities of the ejected electrons increased with the frequency of the light. What if the velocities of the electrons were based upon half-waves of light providing their ejections? This might explain the paradox.
The answer is that all of the experimenters were correct. Momentum is "mv" and "v" is relative. As the half-wave passes by we see only the "v" relative to us. It can be to the left or to the right, but it must be one or the other. Between half-wave passages, and relative to us, the mass of the ripple is moving tangentially in one direction at velocity "v". Its momentum is "mv" relative to us. After the next half-wave passage, relative to us, the mass of the ripple is moving in the opposite direction at velocity "v" with momentum equal but in the opposite direction relative to us. We only see momentum as "mv" after each passage of a half-wave.
If we go back to the beginning of the momentum at the electron Schwarzschild radius, we find that it is equal to me(ts/t)c relative to us. This is precisely the correct momentum relative to us, but it will be in only one of two directions that oppose one another. So what Compton measured was what we can see relative to us - which is half what it should be in the strictest sense. The actual change in momentum is
2me(ts/t)c.
Click on the following for more information.
Back to Electromagnetic Radiation
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding n - The Planck Area
Discussion and Conclusions -
Summary of Mathematical Findings
h = accepted Planck's constant
(dimensionally h = madt)
f = frequency
me = Mass flow
a = acceleration,
c = the speed of light
ts = time of nether direction change during the electron turn-around
when creating a light half-wave
d = distance over which the acceleration of 2c/ts moves nether inflow
Looking at the half-wave equation where dimensionally
h/(2t) = mad we see
h/(2t) = mad
h/(2t) = [me(ts/t)](2c/ts)(cts/2)
h/(2t) = me(ts/t)c2
h/2 = metsc2
Solving for "ts"
ts = h/(2mec2)
ts = 4.12702x10-22 second
If what I consider to be the correct Planck's constant is used, then dimensionally:
h/2 = mad
h/2 = [me(ts/t)](2c/ts)(cts/2)
h/2 = [me(ts/t)]c2
ts = ht/(2mec 2)
ts = 4.12702x10 -22 second
Either way, ts is the same.
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings Looking at the half-wave equation in another way, the term "d", used for a certain distance over which the movement "2c/ts" is applied, is actually the sum of many distances divided by two, each of of which is a circumference of the circle formed at rs, and also forming a dimension of the Mass that is moved to create the half-wave for light. The Mass is strangely shaped because the inward movement of the first part of the acceleration that is the half-wave begins when the electron is beginning to rotate, and the first part of the the half-wave is, therefore, starting its journey earlier than the other portions of the half-wave. So "d" is a means of summing up half of the the number of vortex "revolutions" during an electron reversal. At the core of the electron it is equal to n(2pi)rs/2. The actual length that is the extra dimension, "S", is n(2pi)rs. However, this length begins to move into the electron center immediately and the first part to move in does not move the distance "S". In fact, only the last part to move in actually moves the full distance. When the math is done, we find that the correct distance, on average, that each part moves it time ts is "S/2". So d = n(2pi)rs/2 = cts/2.
h/(2t) = [me(ts/t)](2c/ts)d
h = 4mecd
Solving for d:
d = h/(4mec)
d = 6.1862x10 -14 meters
d = n(2pi)rs/2 = n(pi)rs at the starting radius for light generation.
n = d/[(pi)rs]
n = 1.4554x10 43
New "Knowns"
Turn-around time for the electron = ts = 4.1270x10 -22 second
Number of vortex revolutions in time ts = n = 1.4554x10 43 revolutions
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n
Discussion and Conclusions - Summary of Mathematical Findings According to one book on late 20th century physics [the comments in the brackets are mine]:
"The Planck length, Lp is estimated (to an uncertainty of 1/13 of a percent) to be 1.6160x10 -35 meter. [This is incorrect but typical.] This is based upon the joule second version of Planck's constant. [Any version that is correct is supposed to obtain the correct answer. I discovered that by using the joule second version of Planck's unit of action with an incompatible version of the gravitational constant, one can arrive precisely at this same incorrect answer.] In general relativity, it is the natural unit of Planck force giving unit acceleration to unit mass, and in general relativity, it is a key to how gravity works. It is the square root of "bar h", shown here as h, multiplied by "c" for the natural force area unit, hc, divided by the natural unit force, c4/G. According to John Baez, a physicist, Planck area, Gh/c3 is even more fundamental than Planck length."
Although poorly written, I believe that the above means
(1) Planck length is supposed to be equal to 1.6160x10-35 meter [not true],
(2) Planck length is the natural unit of Planck force,
(3) Planck force is the key to how gravity works (in general relativity),
(4) Planck force gives acceleration to unit mass,
(5) hc is the natural force area unit,
(6) the natural unit force is c4/G,
(7) Planck area is (hc)/(c4/G),
(8) Planck area is, therefore, equal to Gh/c3,
(9) Planck length is the square root of Planck area.
Frankly, I don't trust that book very much as I have found errors in it
before.
The value given for the half-wave equation above can be used with rs in a
derivation as follows.
h/(2t) = [me(ts/t)](2c/ts)d
h = 4mecd
Solving for d where ns is revolutions at rs :
d = h/(4mec)
Going back to the equation for the Schwarzschild radius,
rs = 2Gm/c2
Solving for m:
m = rsc2/2G
d = h/(4mec) Substituting:
d = h/[4c(rsc2/2G)]
d = Gh/(2rsc3)
d(2rs) = Gh/c3
d = n(2pi)rs/2 = n(pi)rs Substituting:
(n(pi)rs)(2rs) = Gh/c3
1. n(2pi)rs2 = Gh/c3
h/(2pi) = h
h = (2pi)h
n(2pi)rs2 = G[(2pi)h]/c3
2. nrs2 = Gh/c3
The above equation has the Planck area on the right.
The Planck area is about 2.6642x10-71 meter2
If the Planck length is the square root of the Planck length, it is about 5.1616x10-36.
Have not yet discovered the significance of equations 1 and 2 above.
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n - The Planck Area
Summary of Mathematical Findings The electron reversing direction is what causes the half-wave of acceleration. Before each reversal the electron is decelerating in its polar direction of movement, and after each reversal the electron is accelerating in its polar direction of movement. During the reversal, the electron vortex is taking in nether at a constant rate, producing a number of "revolutions" of nether entry equal to "n" which is the effect that creates the half-wave acceleration of light.
The question arises as whether or not there is a way to crosscheck the value of "ts".
The half-wave energy passes into the receiving electron in about 2x10-22 second. This is a distance of about (3x108)(2x10-22) which is approximately 1x10-14 meters or a ten-thousandth of an angstrom.
The highest known frequencies are about 1x1022. These have half-wavelengths that are essentially the same (within the limits of our ability to measure them) as the distance for the electron to travel after its turn each time. Apparently, the electron requires a certain space or time to make its turn and that is the reason for the time used which is called "ts" here.
"ts" should be the time used to make one half-wave of the highest possible frequency. Therefore, the inverse of the highest known frequency multiplied by 2 should be equal to ts. The inverse of the frequency for the highest known gamma radiation appears to be very close to the correct value.
It should be remembered that the half-wave of acceleration, that is part of what we call a photon, moves outward at what is literally a crawl at the beginning and builds up speed as the distance from the electron center increases.
It seems that when producing a typical series of light waves (not the highest frequencies) the source electron sends a light half-wave as it changes direction, moves a distance and changes direction once more, sends another half-wave, and so on. The portion of the half-wave of acceleration that is received is the same for any frequency and is caused by n complete revolutions of nether entering the vortex. The distance the electron travels between sending the new acceleration through the nether is what governs the frequency or distance between half-wave receptions.
The Schwartzschild radius for the electron may not show the true radius where the incoming nether is to equal to "c". The electron is a vortex creating a tiny gravity funnel with a cross-section, at the magnitude of rs, that is a hemisphere. The usual gravity funnel has a cross-section that is spherical. So the electron must have a vortex radius at incoming nether velocity "c" that mimics the effect of a spherical cross-section. In other words, the cross-section at incoming nether velocity "c" may be required to have the same area as would a spherical cross-section at incoming nether velocity "c". This means that the actual rs of the electron is probably close to the product of the square root of two and its supposed rs. This radius can be called re.
Regardless, it is the rs rather than the re or the actual hole radius that should be the basis of the flow into the hole for purposes of these calculations.
According to my experiments with vortices, the actual radius of the hole into the 4th dimension should be double the value of re and can be called rh.
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n - The Planck Area
Discussion and Conclusions What follows is a list of the relevant values found rounded to four digits after the decimal point (because further digits are probably not very correct).
Speed of Light = c = 2.9979x10 8 meters/second
Electron Mass = me = 9.1096x10 -31 kilogram
where the *kilogram is a unit of mass
Planck's Constant = h = 6.6252x10 -34 Joule second
= 6.7577x10 -35 meter
kilogram second
where the *kilogram is unit of force
The units for Planck's constant are flawed. See Planck's Constant.
Planck Unit of Action = h = h/(2pi)
= 1.0544x10 -34 Joule second = 1.0755x10 -35 meter
kilogram second
where the *kilogram is a unit of force
Planck Area = Ap = 2.6641x10 -71 meter 2
Planck Length = Lp = 5.1615x10 -36 meter
Gravitational Constant = G = 6.6742x10 -11 meter3/kilogram second2
where the *kilogram is unit of mass
Computed electron Schartzschild radius = rs = 1.3530x10 -57 meter
Possible actual electron Radius at "c" = re = 1.9134x10 -57 meter
Possible hole Radius = rh = 3.8267x10 -57 meter
Time for incoming nether Mass to create the light half-wave
= ts = 4.1270x10 -22 second
(The time for one turn-around of the electron when creating light.)
A product that remains constant = nrs = nere = 1.9661x10 -14 meter revolutions
Number of vortex revolutions at radius rs in time ts = n = 1.4554x10 43 revolutions
Number of vortex revolutions at radius re in time ts = ne = 1.029x10 43 revolutions
Incoming Mass seconds in time ts = Ms =
3.7595x10 -52 kilogram second
where the *kilogram is a unit of mass.
Incoming Mass seconds in one electron vortex revolution at rs =
Mas = 2.5832x10 -95 kilogram second
where the *kilogram is a unit of mass.
Incoming Mass seconds in one electron vortex revolution at re =
Mae = 3.6531x10 -95 kilogram second
where the*kilogram is a unit of mass.
*The metric system has the same name for force as for mass, unlike the English system which uses pounds for force and slugs for mass. The metric system was devised to create a standard that was "natural". Actually, the metric system is erroneous as to the "natural" part and fails to properly address the difference between force and mass. Perhaps it could be improved by calling the force unit a "Kram" and keeping the mass unit as the "gram".
When working on this part of the website, I was constantly spending more time converting units, checking and re-checking the conversions, than I was spending with the theory itself. Our systems of measurement came about from different branches of science in different countries at different times and they do not easily work with one another. In fact, measuring systems are much like committees. The more there are, the more is the obstruction of progress and the obfuscation of thought. It may be said that what we have created is an abomination that is a non-system. Perhaps we can eventually find a way to have a reasonable standard system of measurement that works with all disciplines of science and engineering.
Back - Main Menu - Confirmation of Light as Waves
Introduction - The Schwarzschild Radius - Vortex Coils and Mass
The Light Equation - Finding ts - Finding n - The Planck Area
Discussion and Conclusions - Summary of Mathematical Findings